인공 신경망의 역사

최근 친구와 '기본'을 주제로 담화를 나눈던 도중

"어린아이나 아는 걸 뭣하러 해야하는가?"라는 핀잔에

"어린아이도 아는 걸 행하지 않으면 무슨 소용이 있겠나?"라는 일침으로

귀한 깨닳음을 얻은 경험이 있습니다.

인공지능을 공부하는 학생으로서

가장 '기본'이 된다고 생각하는 내용을 정리해 보았습니다.

 

인공 신경망을 다루기 전 생물학적 뉴런에 대해서 먼저 살펴봅시다.

 

생물학적 신경망

왼쪽에 보이는 그림은 생물학적 뉴런을 나타냅니다. 동물의 뇌에서 발견됩니다.

각각의 뉴런 세포는 짧은 전기 자극을 만들어내어 다른 뉴런에게 전달합니다.

하나의 뉴런은 단순하게 동작하지만, 보통의 뇌는 수십억개의 뉴런으로 구성되어 유기적으로 동작합니다.

 

이에 착안하여 최초로 뇌를 모방한 단순한 신경망 모델을 제시하였는데,

이것이 나중에 인공 뉴런(Artifical neuron)이 되었습니다.

 

---

 

인공뉴런 - 매컬러 & 피츠 (1940s)

 

 

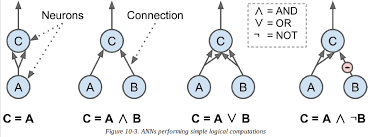
뉴런을 사용한 논리연산

 

• 이진 입력과 이진 출력을 갖습니다.
• 단순히 입력이 일정 개수만큼 활성화되었을 때 출력을 내보냅니다.
• 둘 이상의 입력이 있어야 뉴런이 활성화됩니다.

 

간단한 모델로 많은 명제를 해결할 수 있습니다.

하지만 복잡한 논리 표현식을 계산하기 위해 위의 네트워크를 사용해야하는지는 의문입니다.

위와 같은 논리 연산은 이미 논리 소자(논리 게이트)가 하는 일입니다.

 

 

퍼셉트론 - 프랑크 로젠블라트 (1957)

 

 

Threshold Logic Unit

 

퍼셉트론은 가장 간단한 인공신경망 구조 중 하나입니다.

퍼셉트론은 TLU(Threshold Logic Unit) 또는 LTU(Linear Threshold Unit)라고 불리는 인공 뉴런을 기반으로 합니다.

 

• 입력과 출력이 (이진 값이 아닌) 어떤 숫자고, 가중치와 연관 되어 있습니다.
• 계산된 합에 계단 함수를 적용하여 출력합니다
• z = (X1 * W1)+(X2 * W2)+...+(Xi * Wi)+...+ (Xn * Wn)

 

퍼셉트론에서 계단함수는 헤비사이드 계단 함수가 사용됩니다.

(헤비사이드 계단 함수 : 임계값을 넘기면 1 그렇지 못하면 0을 출력하는 간단한 함수 입니다.)

예측하고자 하는 문제가 선형적인 양상을 보인다면 정답에 수렴합니다.

 

하지만, 각각의 입력값에 가중치를 곱하여 출력하는 형태입니다. (WX1 + WX2 + ... + WXn)

즉, 각 뉴런의 출력은 선형이므로 퍼셉트론은 복잡한 패턴을 학습하지 못합니다.

 

또한 퍼셉트론에는 심각한 약점이 있습니다.

XOR(배타적 논리합)같은 간단한 문제를 풀 수 없습니다.

 

다층 퍼셉트론 - 마빈 민스키, 시모어 페퍼트 (1969)

 

다층 퍼셉트론 (MLP)

기존의 퍼셉트론 구조로서는 XOR 같은 배타적 논리합 문제를 풀 수 없습니다.

실은 이는 당연합니다. 다수의 양의 값을 입력으로 받으면 양의 값을 출력하는 것이 보통입니다.

 

이는 선형함수의 태생적 특징입니다.

하지만 퍼셉트론을 여러개 쌓아올린다면 어떨까요?

 

하나의 퍼셉트론이 하나의 선형함수를 나타내듯이

입력 값을 공유하는 두 개의 퍼셉트론의 출력값을,

또 다른 퍼셉트론의 입력 값으로 사용한다면

 

두 개의 선형함수의 특징을 모두 아우를 수 있습니다.

퍼셉트론을 여러 개 쌓아 올리면 XOR와 같은 일부 문제를 해결할 수 있다는 사실이 밝혀졌습니다.

 

위와 같은 구조를 다층 퍼셉트론(MLP)이라 합니다.

 

 

역전파 - 제프리 힌턴, 데이비드 루멜하트 (1986)

 

 

역전파

 

퍼셉트론을 여러겹 쌓아올린 형태의 신경망은 성능면에서 개선되었을지 몰라도

각각의 노드를 학습하는 일은 어려워졌습니다.

 

몇 개의 퍼셉트론에 대한 가중치를 일일이 적용해 보는 일은 해볼만한 일이 었어도,

기하급수적으로 늘어난 퍼셉트론의 가중치를 하나씩 부여해 보는 작업(Brute Force)은 어려웠습니다.

랜덤하게 때려 넣어서 적당히 괜찮은 값을 선택하는 일(Monte carlo) 또한 실효성이 떨어졌습니다.

 

이후, 각각의 가중치가 결과 값에 얼마나 영향을 주었는지를 계산하여 반영하는 알고리즘이 고안되었는데

이를 역전파(Backpropagation)라고 합니다.

 

• 정방향 한 번, 역방향 한번 통과하는 것으로 파라미터에 대한 기울기를 계산
• 출력 이후 오차를 측정하여 가중치가 이 오차에 기여한 정도를 계산한 후 가중치를 수정
• 미분을 위해 활성화 함수를 시그모이드 함수로 변경

 

거꾸로 출력층에서 입력층으로 되돌아가며 가중치를 수정합니다.

이 역전파 알고리즘은 각각의 오차에 대한 기울기를 계산할 수 있습니다.

기울기를 계산하고 나면, 경사하강법을 이용하여 오차를 경감하는 일이 가능해 졌습니다.

 

이 알고리즘을 잘 동작시키기 위해서 활성화 함수를 변경하였습니다.

 

계단 함수와 시그모이드 함수

 

계단함수는 수평선 밖에 없으니 계산할 기울기가 없습니다.

이전까지 사용하였던 계단함수를 뒤로하고, 시그모이드 함수를 사용하였습니다.

 

이제 다층 퍼셉트론은 복잡한 논리연산을 수행할 수 있게 되었고,

각각의 가중치를 계산하는 일에도 부담을 덜었습니다.

 

 

그렇다면 아래와 같은 신경망도 학습시킬 수 있는걸까요?

세상에 이게 모람...

 

 

 

딥러닝 - 제프리 힌턴 (2006)

 

기울기 소실

 

위에서 이야기한 것처럼 역전파 알고리즘은 출력층에서 입력층 쪽으로 오차 기울기를 계산하며 나아갑니다.

하지만 역전파가 진행될수록 오차 기울기는 0에 수렴하여 미분 값을 얻어내기 어려워 집니다.

 

하위층으로 가면 갈수록 역전파는 점점 약해져 아래쪽 층에는 아무것도 도달하지 않게 됩니다.

 

이는 활성화 함수의 본질적인 특성에서 기인합니다.

시그모이드 함수의 한계

 

이전까지는 활성화 함수로 시그모이드 함수를 사용해 왔습니다.

 

시그모이드 함수는 양쪽 끝으로 향할수록 기울기가 0 에 수렴합니다.

 

또한 시그모이드 함수의 도함수는 최대 값이 0.3인데, 이는 역전파를 거듭할수록 기울기를 반의 반씩 깍아먹는 셈입니다.

 

하여, 시그모이드 함수를 대체할만한 활성화 함수를 모색하였습니다.

 

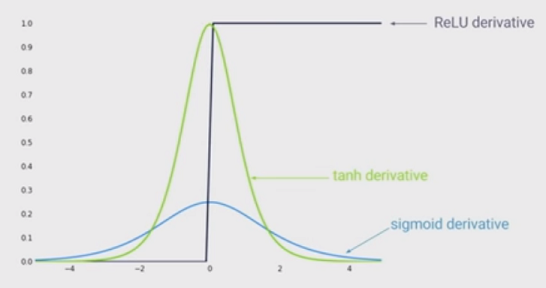
그리하여, 도함수 최대 값이 1.0 에 달하는 하이퍼볼릭 탄젠트 함수(tanh)와

연산 비용이 적고, 함수 값을 그대로 보존하는 ReLU함수가 제안되었습니다.

---

References

• nittaku.tistory.com/265
• jinseob2kim.github.io/deep_learning.html
• www.slideshare.net/HyungsooRyoo/ss-80388094
• times.kaist.ac.kr/news/articleView.html?idxno=4675